这个知识点很重要，但是，我不懂。

        第一个问题：为什么要做正则化？

In mathematics, statistics, and computer science, particularly in the fields of machine learning and inverse problems, regularization is a process of introducing additional information in order to solve an ill-posed problem or to prevent overfitting. 

And, what is ill-posed problem?... ...

And, what is overfitting? In statistics, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit additional data or predict future observations reliably", as the next figure shows. 

Figure 1.  The green curve represents an overfitted model and the black line represents a regularized model. While the green line best follows the training data, it is too dependent on that data and it is likely to have a higher error rate on new unseen data, compared to the black line.

        第二个问题：常用的正则化方法有哪些？

        第三个问题：The advantages fo Tikhonov regularizatioin

        The fourth question: Tikhonov regularization

        Tikhonov regularization, named for Andrey Tikhonov, is the most commonly used method of regularization of ill-posed problems. In statistics, the method is known as ridge regression, in machine learning it is known as weight decay, and with multiple independent discoveries, it is also variously known as the Tikhonov–Miller method, the Phillips–Twomey method, the constrained linear inversion method, and the method of linear regularization. It is related to the Levenberg–Marquardt algorithm for non-linear least-squares problems.

        Suppose that for a known matrix A and vector b, we wish to find a vector x such that:

        

        The standard approach is  linear regression. However, if no x satisfies the equation or more than one x does—that is, the solution is not unique—the problem is said to be . In such cases, ordinary least squares estimation leads to an  (), or more often an  () system of equations. Most real-world phenomena have the effect of  in the forward direction where A maps x to b. Therefore, in solving the inverse-problem, the inverse mapping operates as a  that has the undesirable tendency of amplifying noise ( / singular values are largest in the reverse mapping where they were smallest in the forward mapping). In addition, ordinary least squares implicitly nullifies every element of the reconstructed version of x that is in the null-space of A, rather than allowing for a model to be used as a prior for . Ordinary least squares seeks to minimize the sum of squared , which can be compactly written as:

          where  is the . 

                                             

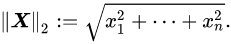
         In order to give preference to a particular solution with desirable properties, a regularization term can be included in this minimization:

         for some suitably chosen Tikhonov matrix, . In many cases, this matrix is chosen as a multiple of the  (), giving preference to solutions with smaller ; this is known as L₂ regularization. In other cases, high-pass operators (e.g., a  or a weighted ) may be used to enforce smoothness if the underlying vector is believed to be mostly continuous. This regularization improves the conditioning of the problem, thus enabling a direct numerical solution. An explicit solution, denoted by , is given by:

, process can be seen at (https://blog.csdn.net/nomadlx53/article/details/50849941).

The effect of regularization may be varied via the scale of matrix . For  this reduces to the unregularized least squares solution provided that (A^TA)⁻¹ exists.

L₂ regularization is used in many contexts aside from linear regression, such as  with  or , and matrix factorization.

     

对于y=Xw，若X无解或有多个解，称这个问题是病态的。病态问题下，用最小二乘法求解会导致过拟合或欠拟合，用正则化来解决。

设X为m乘n矩阵：

• 过拟合模型：m<<nm<<n，欠定方程，存在多解的可能性大；
• 欠拟合模型：m>>nm>>n，超定方程，可能无解，或者有解但准确率很低

 

 

REF:

https://blog.csdn.net/darknightt/article/details/70179848